一 加
在实现加运算前,先了解三个位运算符,位运算表示将整数转换成二进制整数再运算。
1 ^异或
异或运算,相同为0,不同为1
1^1=0 0^0=0 1^0=1 0^1=1
3^4=0000 0011^0000 0100=00000111=7
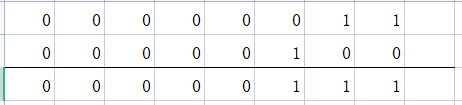
在二进制运算中间 01+01=10 1^1=0
所以^运算相当于没有进位的加法运算。
2 &与
与运算,1&1=1 其他都是0
3 <<左移
二进制整体向左移动一位,原来最高位溢出,最低位补0
3<<1=6

整数3左移一位变成6
(0001&0001)<<1=0001<<1=0010
与和左移两个运算符相结合,相当于进位。由于<<运算符优先级高于&,所以&运算必须有()
所以加运算可以分解成两步,第一步计算没有进位的加(异或),第二步计算进位(与和左移)。再将两个计算结果进行加运算。由于不能使用加运算符,所以将两个结果重复的使用第一步和第二步运算,直到进位为0.
6+4
第一次运算:6^4 + (6&4)<<1 = 0110^0100 + (0110&0100)<<1 = 0010 + 1000 = 2 + 8
6^4没有进位的加 (6&4)<<1 进位
2+8
第二次运算:2^8 + (2&8)<<1 = 0010^1000 + (0010&1000)<<1 = 1010 + 0000 = 10 + 0
因为进位的结果为0,所以不需要进行第三次运算
代码实现:
package com.wanmait;
public class Mathematic {
public int plus(int x,int y)
{
int temp = x^y;//按位异或 没有进位的相加运算
int carryBit = (x&y)<<1;//按位与 并且左移一位 进位
//<<优先级高于&
if(carryBit==0)//没有进位了 结束
{
return temp;
}
return this.plus(temp, carryBit);
}
}二 减
减就是加一个相反数,所以只要求出相反数,就变成了加
求相反数需要用到取反运算符
1 ~取反运算
取反运算符就是原来为1的变成0,原来为0的变成1
~7 = ~ 0000 0111 = 1111 1000
负数采用的是补码的形式 也就是1111 1000 的原码是1000 1000 就是-8
所以相反数就是取反+1
所以x-y = x+ (~y+1)
代码实现:
package com.wanmait;
public class Mathematic {
public int minus(int x,int y)
{
y = ~y;//取反
y = this.plus(y, 1);
//y变成-y
return this.plus(x, y);
}
public int plus(int x,int y)
{
int temp = x^y;//按位异或 没有进位的相加运算
int carryBit = (x&y)<<1;//按位与 并且左移一位
//<<优先级高于&
if(carryBit==0)//没有进位了 结束
{
return temp;
}
return this.plus(temp, carryBit);
}
}











0条评论
点击登录参与评论