宽度优先搜索算法-广度优先搜索

以某点为中心，向四周扩散搜索，直到找到结果为止。

利用该算法搜索迷宫从起点到终点的最优路径.

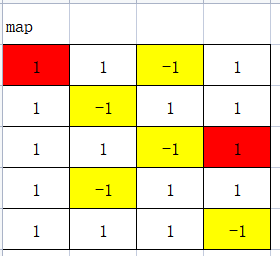
假设有一个上图的迷宫，1表示该点是通路，可以通过，-1表示该点有障碍，不能通过。红色表示迷宫的起点和终点。以上图为例，坐标0:0就是起点，坐标2:3就是终点.

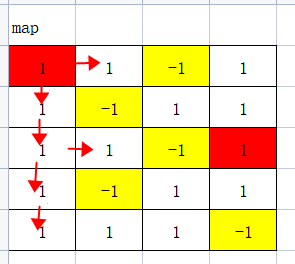
从起点开始，往外扩展，直到找到终点位置.

程序设计：

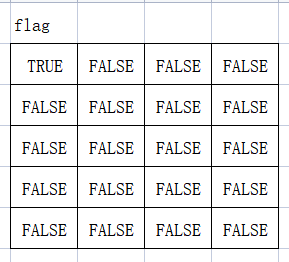
设计flag布尔型数组，用来表示对应的迷宫的格子是否已经访问过，值为false，表示对应的迷宫的格子没有访问过，访问过之后，改为true。

设计step二维数组，分别表示以某点为中心，周围4个点的下标的变化

Cell类表示迷宫的一个格子,x和y表示格子的坐标,stepCount表示到达该格子的步数，pre表示到达该格子之前的格子.

listCell队列，用来保存目前正访问的迷宫的格子.

代码：

cell.java

package com.wanmait;

public class Cell {
	private int x;//格子的坐标
	private int y;
	private int stepCount;//第几步
	private Cell pre;//上一个格子
	
	public Cell(int x,int y,int stepCount) {
		this.x = x;
		this.y = y;
		this.stepCount = stepCount;
	}
	public void setPre(Cell pre)
	{
		this.pre = pre;
	}
	public Cell getPre() {
		return this.pre;
	}
	public int getX() {
		return x;
	}
	public void setX(int x) {
		this.x = x;
	}
	public int getY() {
		return y;
	}
	public void setY(int y) {
		this.y = y;
	}
	public int getStepCount() {
		return stepCount;
	}
	public void setStepCount(int stepCount) {
		this.stepCount = stepCount;
	}
}

Demo.java

package com.wanmait;

import java.util.LinkedList;

public class Demo {
	private int map[][];//地图  1 表示可以行走  -1 表示不能走
	private int startx,starty,endx,endy;//起点下标  终点下标
	private boolean flag[][];//标记对应的点是否走过
	private int step[][] = {{0,1},{0,-1},{1,0},{-1,0}};//某个格子周围4个格子的坐标变化的值
	
	//显示从起点到终点的最有路径的格子的坐标
	public void showPath(Cell cell) {
		System.out.println(cell.getX()+":"+cell.getY());
		if(cell.getPre()!=null) {
			this.showPath(cell.getPre());
		}
	}
	
	//x和y起点坐标
	public void go(int x,int y)
	{
		Cell cell = new Cell(x,y,0);//起点
		LinkedList<Cell> listCell = new LinkedList<>();//保存经过的格子
		listCell.add(cell);//起点保存到队列
		flag[x][y] = true;
		boolean f = false;//是否到达终点
		
		while(!listCell.isEmpty()) {
			Cell first = listCell.getFirst();//取队列的第一个元素
			if(first.getX()==endx&&first.getY()==endy)//到达终点 
			{
				System.out.println("步数:"+first.getStepCount());
				this.showPath(first);
				f = true;
				break;
			}
			
			//first格子的周围4个格子
			for (int i = 0; i < 4; i++) 
			{
				int newx = first.getX()+step[i][0];
				int newy = first.getY()+step[i][1];
				int stepCount = first.getStepCount()+1;
				
				if(newx<0||newx>4||newy<0||newy>3)
				{
					continue;
				}
				
				if(map[newx][newy]==1&&flag[newx][newy]==false) {
					Cell temp = new Cell(newx,newy,stepCount);
					temp.setPre(first);
					listCell.add(temp);
					flag[newx][newy] = true;
				}
			}
			
			listCell.removeFirst();
		}
		
		if(f==false) {
			System.out.println("无法到达终点");
		}
	}
	
	//初始化
	public void init()
	{
		flag = new boolean[5][4];
		
		map = new int[5][4];
		map[0] = new int[] {1,1,-1,1};
		map[1] = new int[] {1,-1,1,1};
		map[2] = new int[] {1,1,-1,1};
		map[3] = new int[] {1,-1,1,1};
		map[4] = new int[] {1,1,1,-1};
		
		startx = 0;
		starty = 0;
		endx = 2;
		endy = 3;
	}
}

main

package com.wanmait;

public class Test {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Demo demo = new Demo();
		demo.init();
		demo.go(0, 0);
	}

}