引言

在开发中，尤其是需要处理大量数据或者进行任务调度的场景下，如何高效地管理数据的顺序和优先级是一个至关重要的问题。Java 提供了优先级队列（PriorityQueue），它基于堆（Heap）实现，能够以高效的方式管理数据的优先级。在本文中，我们将深入探讨优先级队列的工作原理，特别是堆的作用，并通过示例代码帮助你更好地理解其应用。

一、什么是优先级队列？

优先级队列（Priority Queue）是一种队列数据结构，其中每个元素都包含一个优先级，队列总是按元素的优先级顺序进行排序。与普通队列（先进先出 FIFO）不同，优先级队列确保每次从队列中移除的元素是具有最高优先级的元素。有些场景下，使⽤队列显然不合适，⽐如：在⼿机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话；初中那会班主任排座位时可能会让成绩好的同学先挑座位。

在 Java 中，PriorityQueue 是基于堆的实现。堆是一种特殊的二叉树结构，满足特定的顺序性质：最大堆保证每个父节点的值大于等于其子节点的值，而最小堆则相反。

二、堆的基本原理

JDK1.8中的PriorityQueue底层使⽤了堆这种数据结构，⽽堆实际就是在完全⼆叉树的基础上进⾏了⼀些调整。具有以下特点：

对于最大堆，父节点的值始终大于或等于子节点的值；

对于最小堆，父节点的值始终小于或等于子节点的值。

2.1 堆的概念

如果有⼀个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全⼆叉树的顺序存储⽅式存储在⼀个⼀维数组中，并满⾜：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为⼩堆(或⼤堆)。

Java 中的 PriorityQueue 默认是最小堆，也就是说队列中最小的元素将具有最高的优先级。

2.2 堆的存储⽅式

从堆的概念可知，堆是⼀棵完全⼆叉树，因此可以层序的规则采⽤顺序的⽅式来⾼效存储，

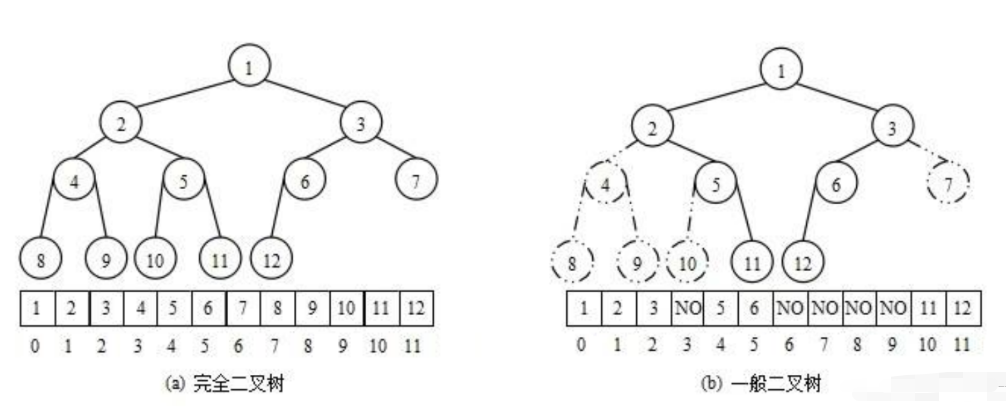
将元素存储到数组中后，可以根据⼆叉树章节的性质5对树进⾏还原。假设i为节点在数组中的下标，则有：

• 如果i为0，则i表⽰的节点为根节点，否则i节点的双亲节点为 (i - 1)/2

• 如果2 * i + 1 ⼩于节点个数，则节点i的左孩⼦下标为2 * i + 1，否则没有左孩⼦

• 如果2 * i + 2 ⼩于节点个数，则节点i的右孩⼦下标为2 * i + 2，否则没有右孩⼦

三、堆操作时间复杂度

3.1 建堆的时间复杂度

因为堆是完全⼆叉树，⽽满⼆叉树也是完全⼆叉树，此处为了简化使⽤满⼆叉树来证明(时间复杂度本
来看的就是近似值，多⼏个节点不影响最终结果)：

因此：建堆的时间复杂度为O(N)。

四、PriorityQueue 的基本操作

1. PriorityQueue中放置的元素必须要能够⽐较⼤⼩，不能插⼊⽆法⽐较⼤⼩的对象，否则会抛出 ClassCastException异常

2. 不能插⼊null对象，否则会抛出NullPointerException

3. 没有容量限制，可以插⼊任意多个元素，其内部可以⾃动扩容

4. 插⼊和删除元素的时间复杂度为

5. PriorityQueue底层使⽤了堆数据结构

6. PriorityQueue默认情况下是⼩堆—即每次获取到的元素都是最⼩的元素

4.1 插⼊/删除/获取优先级最⾼的元素

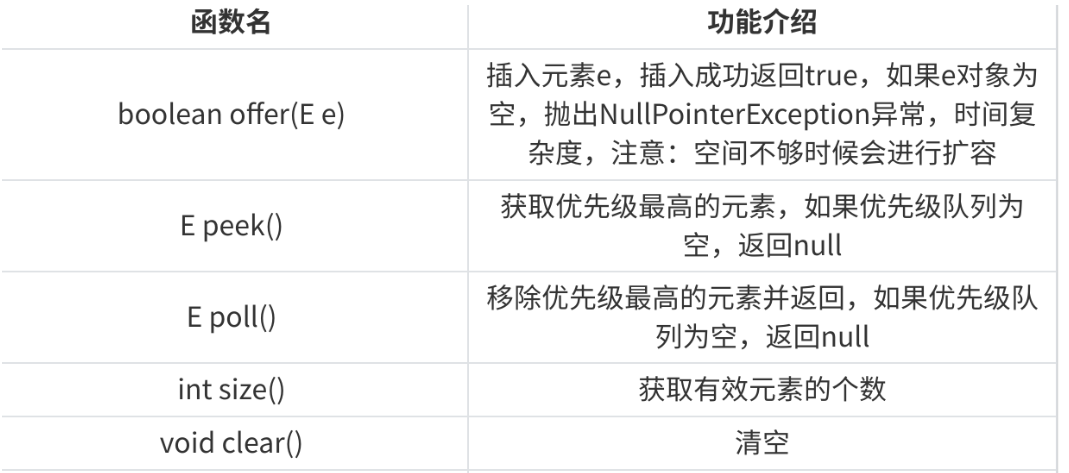
注意：优先级队列的扩容说明：

• 如果容量⼩于64时，是按照oldCapacity的2倍⽅式扩容的
• 如果容量⼤于等于64，是按照oldCapacity的1.5倍⽅式扩容的
•如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进⾏扩容